|
◆ 밀러 지수(Miller-lndex)
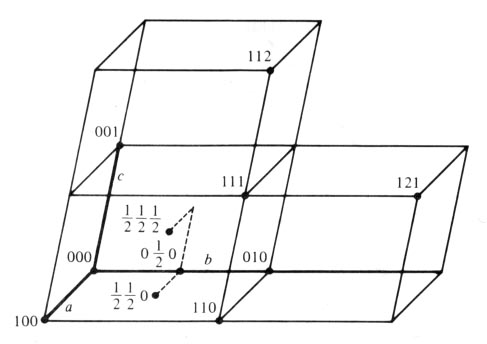
그림
2와 같이 입방정의 단위격자의 한 모서리점을
원점으로 하여 3차원의 좌표계를 생각하고 격자상수를
단위로 하여 원점으로부터의 거리로 나타내면 각
원자의 위치는 그림에 표시한 바와 같이 결정된다.
그러나 결정구조의 대칭성과 반복성 때문에 개개의
원자위치를 나타내는 것보다다는 원자로 구성되는
면이나 원자배열의 방향을 상대적으로 나타내는 것이
훨씬 편리하다. 변이나 방향의 표시는 결정학에서
사용되는 밀러지수를 사용하는 것이 편리하므로
밀러지수를 결정하는 법을 알아보기로 하자.
그림
2. 원자위치의 좌표
결정면의
밀러지수는 면에 의해 교차되는 좌표축의 길이를
그축의 단위길로로 나눈 값의 역수의 최소 정수비로
나타내며 그 지수가 h, k, l이라면(hkl)로 쓴다.
결정방향의
밀러지수는 방향인 나타내는 직선이 원점을 지난다고
가정할 때 직선상에 있는 임의의 한점의 좌표의
최소정수비로 나타내며 그 지수가 u, v, w라면 [uvw]로
나타낸다. 또 지수가 음의 값을 갖는 경우에는
숫자위에 마이너스 부호를 붙여서 (hkl) 또는 [uvw]와
같이 나타낸다. 여기서 좀 더 이해를 쉽게
하기 위해 금속의 결정으로 중요한 입방정계와
육방정계에 대하여 실례를 들어 설명하기로 한다.
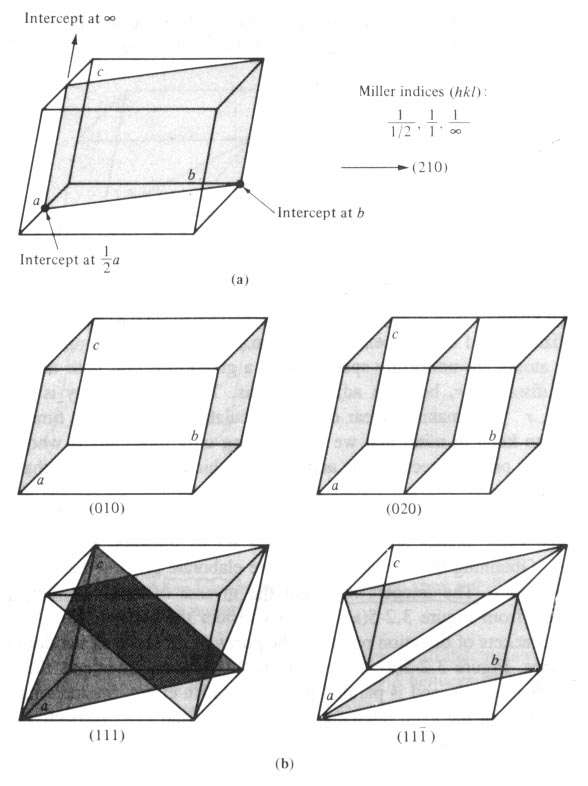
그림
3. 일반적인 평면 및 서로 평행한 면의 밀러지수
①
입방정계의 경우
그림 3을
고려하면
x,
y, z축의 절편의 길이 4, 3, 2
역수를
취하면 1/4, 1/3, 1/2
이들의
최소정수비는 3, 4, 6
따라서 이 면의
밀러지수는 (3 4 6)이 된다. 또한 그림 3에서의 같은
평행면을 생각하면
면A
면B 면C
절편의
길이 1, 1, 1 3,
3, 3
-1, -1, -1
역수
1,
1, 1 1/3, 1/3, 1/3
-1, -1, -1
밀러지수
(111)
(111)
(iii)
따라서
평행한 면은 같은 지수로 나타낼 수 있으며 그림에서
알 수 있듯이 (111)면과 (111)면 처럼 지수가 같고 부호가
전부 반대인 면도 평행이다. 면이 좌표축과 평행한
경우는 수학적으로 좌표축의 절편이 무한대가 되어
지수는 0이 된다. 여기서 유의할 점은 결정격자의
규칙성 때문에 좌표축의 원점을 어느 곳에 설정해도
같은 관계가 성립해야 한다는 점이다.
앞서
언급한 바와 같이 결정격자 내에서 같은 지수를 갖는
면은 무수히 많으며 그들의 면간 거리는 항시
일정하다. 원자밀도는 일반적으로 면지수가 큰
면일수록 면간거리는 작게 되고 또 그 면의
원자밀도도 작게 된다.
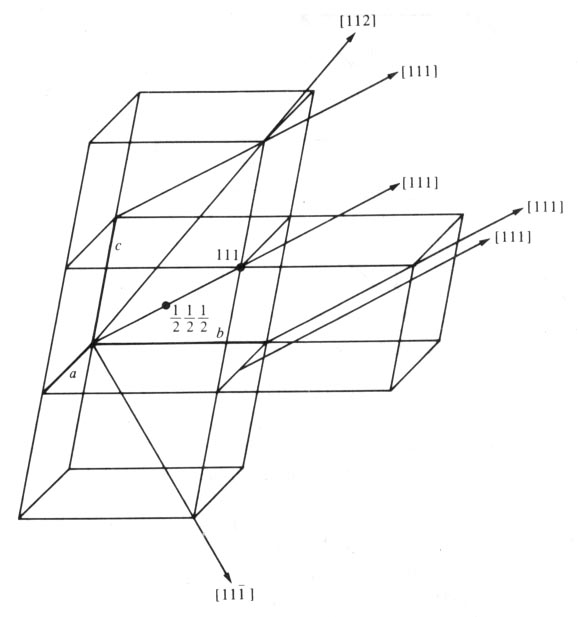
그림
4. 방향의 밀러지수
방향을
나타닐 때에는 그림 4에 나타낸 바와 같이 그 방향과
평행이고 원점을 지나는 직선을 생각하고 그 위에
적당한 점 A를 택하면, 그 점의 좌표가 방향의
밀러지수가 된다. 그림에서는 A점의 좌표가 2, 1, 1이므로
밀러 지수는 [211]이라고 스며 만일 직선상의 점 B를
택했다면 B점의 좌표는 4, 2, 2가 되나 밀러지수는
최소점수비를 택하므로 [211]이 된다. 따라서 이 직선과
평행한 모든 방향은 같은 지수로 나타낼 수 있다.
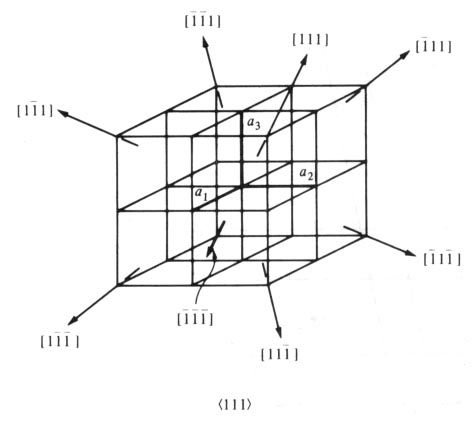
그림
5. 입방정계의 주요면에서의 방향지수
그림
5에는 입방정계에 있어서 중요면과 방향의 지수를
나타냈다. 그림에서 [100]방향과 (100)면, [110]방향과 (110)면의
관계에서 알 수 있듯이 입방정계에서는 면과 방향의
지수가 같을 경우 반드시 직교한다. 또한 (100), (010),
(001) 등의 면은 좌표축에 대한 상대적 대칭성은 똑
같다. 이같이 상대적인 대칭성이 같은 면이나 방향을
결정학점으로 등가(equivalent)라고 부르며, 등가인
일군의 방향을 <uΩw>로 쓰며 여기서 < >는
방향족(family of directions)을 나타낸다. 마찬가지로
등가인 일군의 면을 {hkl}로 쓰며 { }는 형면족(family of
planes)을 나타내며 이러한 기호로 표시되는 모든
등가한 면이나 방향은 지수의 순서 및 부호를
바꿈으로써 얻을 수 있다. 예를 들어 {100}면은 (100),
(01), (001), (100), (010), (001)의 6개의 면을 품는다. 그러나
앞서 말했듯이 지수가 같고 부호가 전부 반대인 면은
평행하므로 결국 3개의 면을 품게 되는 것이다. 따라서
다음과 같이 쓸 수 있다.
{111}={(111),
{111}, {111}, {111}}
<110>={[110],
[101], [01], [11]0, [101], [011]}
또한
입방정계의 면 중에서 {100}면을 입방체면(cubic plane)
{110}면을 12면체면(dodecahedral plane), {111}면을 8면체면(octahedral
plane)이라 부르기도 한다.
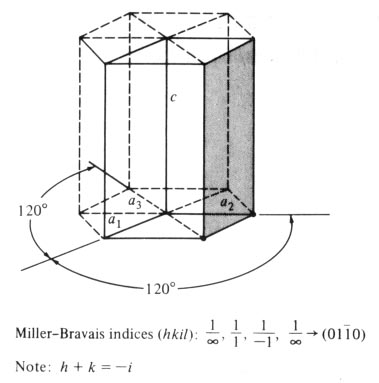
그림
6. 육방정계의 좌표축과 밀러-브라바이스 지수
② 육방정계의
경우
육방정계에서도
면지수 및 방향지수가 적용될 수 있다. 그림 6에
나타낸 바와 같이 육방격자의 단위표는 같은 평면에서
120°로 고차하고 있는 a1, a2, a3축과
이 평면에 수직한 c축을 갖고 있다. 따라서 육방정계의
면지수 및 방향지수는 이 4개의 축에 대응되는 4개의
지수가 필요하다.
육방정계의
면지수는 (hkil)로 표시되며 이 지수를 Miller-Bravais지수라고
한다. 여기서 h, k, i는 각각 a1, a2, a3축과
그리고 l은 c축과 만나는 점까지의 길이와 단위길이에
대한 비의 역수의 최소정수비가 된다. 그러나
그림에서 알 수 있듯이 i는 h와 k로 나타낼 수 있으며
h+k=-i의 관계가 성립한다. 따라서 (hkil)을 (hkl)로 나타낼
수 있다.
육방정계에서
대표적인 면은 기준면(base plane)인 {0001}면, 각통면(prismatic
plane)인 {1010}면, 각뿐면{pyramidal plane)인 {1011}면이 있다.
육방정계의
방향도 앞서 설명한 바와 같이 4개의 축에 의해
결정되므로 {uvtw]와 같이 표시되나 면지수와
마찬가지로 u+v=-t의 관계가 성립하므로 [UVW]로 표시할
수 있으며 이때의 변환 [uvtw] → [UVW]는
U=u-t
V=v-t
W=w
에 의해
행하여진다. 예를 들면
[1011]=[211],
[2110]=[320], [1120]=[330]=[110]이다.
육방정계에서는
같은 지수를 갖는 면과 방향의 직교성이 수직축에
평행한 면에서만 성립된다.
|